Throughout a variety of courses in engineering and mathematics, educators have struggled to determine effective ways to deliver technically rigorous, conceptually accessible, and cognitively engaging content to students. Because of this, one of these criteria is often sacrificed. As an undergraduate STEM major, I noticed this phenomenon occur particularly with respect to teaching modalities. In a classroom setting, professors who emphasize course austerity commonly lack student relatability, and those who do manage to connect with students’ understanding end up repeatedly diminishing crucial content. However, this dilemma is not exclusive to instructors. For many college students, presentations, be it for a class project or undergrad research, face a similar scrutiny. Seeing such an alarming pattern repeated over and over again in different settings, I decided to make mental notes of certain components in a lecture or presentation that were lacking so that I could avoid these same mistakes. Over time, I developed a comprehensive list of six key characteristics that I felt should be employed, when relevant, to produce a presentation that utilizes various instructional modalities, while also delivering content that is both challenging and engaging. In particular, I was able to use these components as a foundational model for my work in undergraduate research and upper-division, STEM education.
Motivations
Understanding why a particular topic is relevant and the reason we are interested in studying it
Procedures
Developing a systematic approach or thought process when strategizing solutions
Definitions
Providing detailed definitions for relevant terms to improve comprehension and implement in problem solving
Examples
Presenting a variety of examples with increasing progression in difficulty or complexity
Mathematics
Utilizing a mathematical foundation as the primary component in conceptual understanding
Visuals
Implementing various visual tools throughout for conceptual reinforcement
In Summer 2019, I participated in my university’s Research Experience for Undergraduates (REU) internship program, which focused on a variety of projects related to energy storage and conversion. Rooted in sustainable energy work, my research focused on mathematical modeling of biomass pyrolysis using discrete element method (DEM). In particular, I was interested in investigating DEM as a computational method that could be used to simulate the microstructural shrinkage of switchgrass during pyrolysis. Although I was thrilled about the mathematically rigorous nature of my research topic, even after daily meetings with my advisor in the first week of the program, I struggled to understand how things like wall forces and matrices full of differential equations were relevant to my work. Finally, after receiving guidance from my dad, who fortunately was familiar with numerical techniques and MATLAB programming, everything began to click. For the following few weeks, I painstakingly wrote hundreds of lines of code, making substantial progress day by day.
About halfway through my internship, the REU director informed us that we were required to give a presentation over our research to the other students and faculty in the program. Wanting to take full advantage of this educational opportunity, I was determined to create a presentation that students could walk away from with a clear and thorough understanding of my work. With that in mind, I developed a PowerPoint and a corresponding lecture that utilized all six of the characteristics listed above. As a result, on my feedback report, 100% of the audience positively reported “Strongly Agree” to my presentation’s organization, ideological flow and conceptual explanations, and use of visuals/illustrations.
Throughout the following months, I continued my research, and in February 2020, I presented my work at the TLSAMP Research Conference at UT Knoxville, where I received 1st Place in the Engineering and Mathematics Poster Competition.

a) Portion of switchgrass microstructure
Source: Rachael Koehler

b) Shrinkage model for circled portion of microstructure developed in MATLAB
After my positive experience in the REU program, I was motivated to seek out a different opportunity that focused primarily on undergraduate STEM education. As a student in the Honors Program at Tennessee Tech, one of our requirements for graduation is to complete various upper-division coursework. One way to accomplish this is by engaging in an advanced, senior-level project related to the student's major and career goals. Seeing this as a chance for me to combine my passion for applied mathematics and undergraduate education utilizing various modalities, I chose to develop a series of presentations for a linear algebra class that I was enrolled in. Every two weeks, I discussed the applications of various concepts in matrix and linear algebra throughout science and engineering. For each 15-minute presentation, I researched specific examples that involved extending basic algebraic concepts involving matrices to challenging and thought-provoking engineering phenomena. I focused primarily on selecting applications that 1) combined content from a variety of mathematics courses and 2) could be demonstrated via visual simulations developed in GeoGebra.
For me, as an engineering student, seeing the practical use of class concepts was a common occurrence. However, I struggled to say the same regarding my experience as a mathematics student. On the other hand, my coursework involving proofs-based, abstract mathematics revealed an almost artistic side of STEM that I had never seen before in chemical engineering. Realizing this, I wanted to ensure that my initial set of presentations touched on both of these ideas.
I began with a lecture sequence that covered the concept of curve fitting. In the first of the two-part series, I focused on a fairly straightforward extension of matrix applications in solving systems of simultaneous equations, where students learned how to fit an n-th degree polynomial to a set of data points and the ways in which matrices can be used to glean certain information about the characteristics of the corresponding curve. Having established a conceptual foundation with the class, the second lecture presentation in the series was where I explored a more advanced application. Here, instead of fitting polynomial curves to a set of known coordinates, I discussed the ways in which matrices can be used to "fit" a second-order, linear, homogeneous, ordinary differential equation to a set of linearly independent functions. Though only slightly more involved than the previous presentation, the integration of differential equations in linear algebra required students to make unique conceptual connections in a novel application.
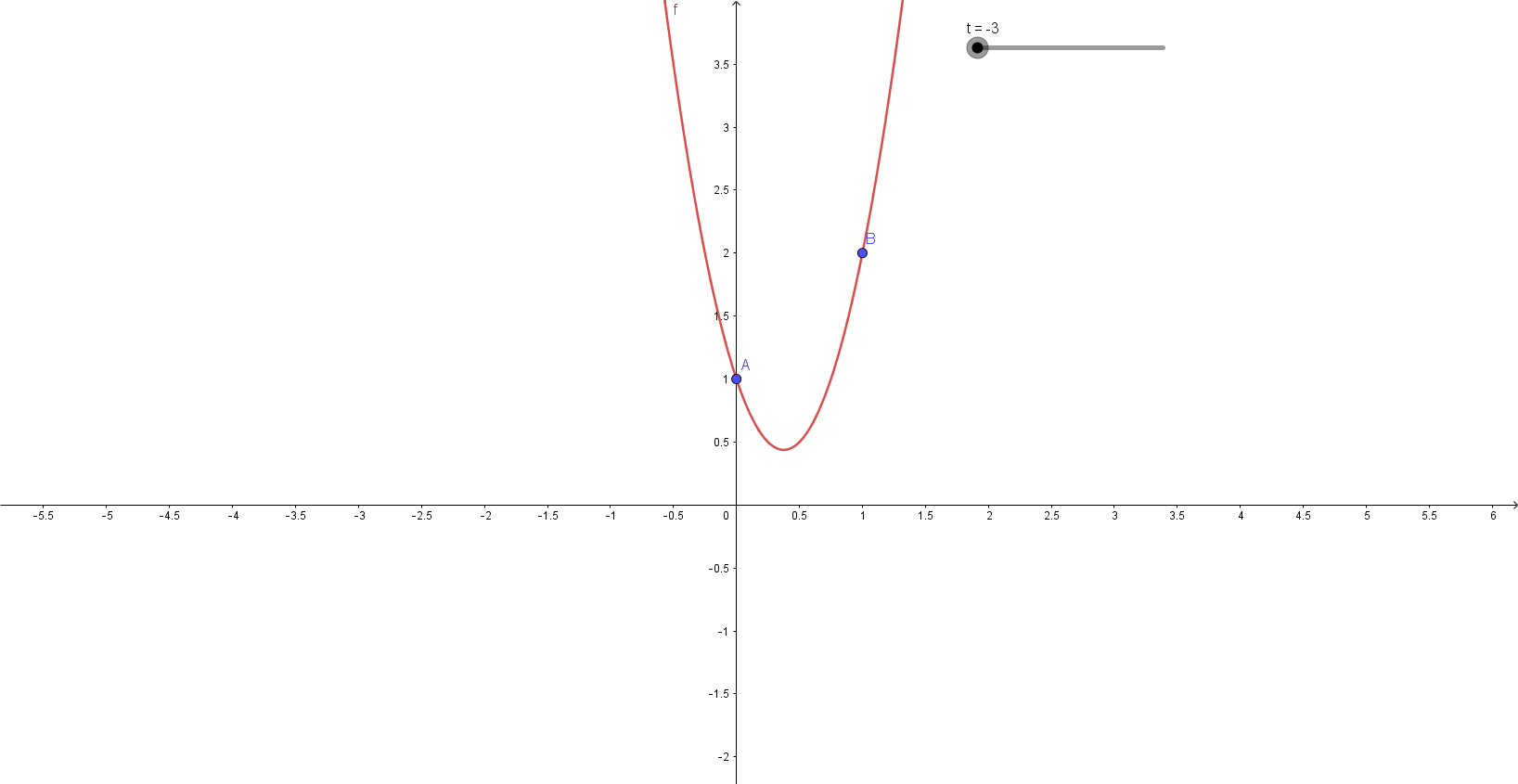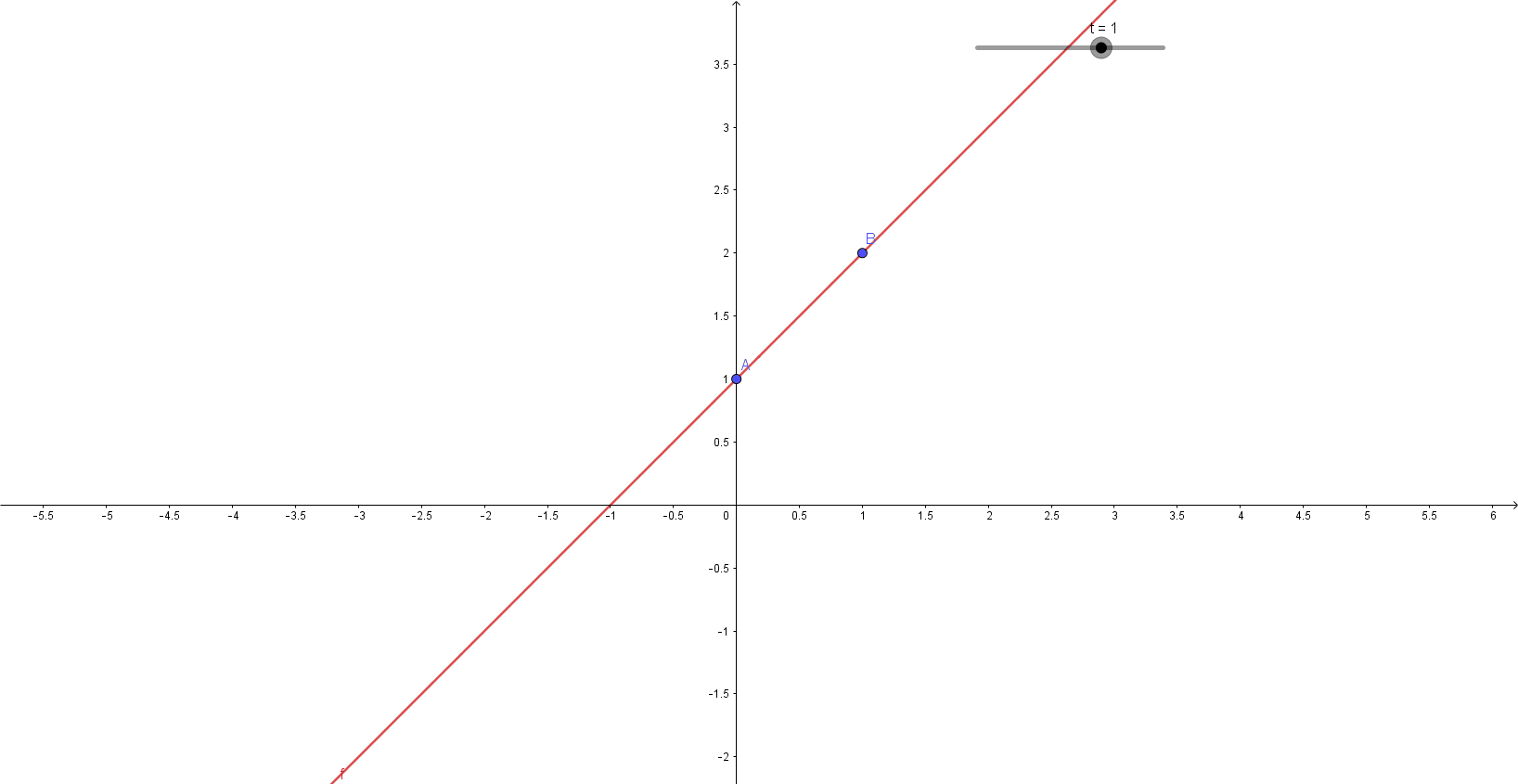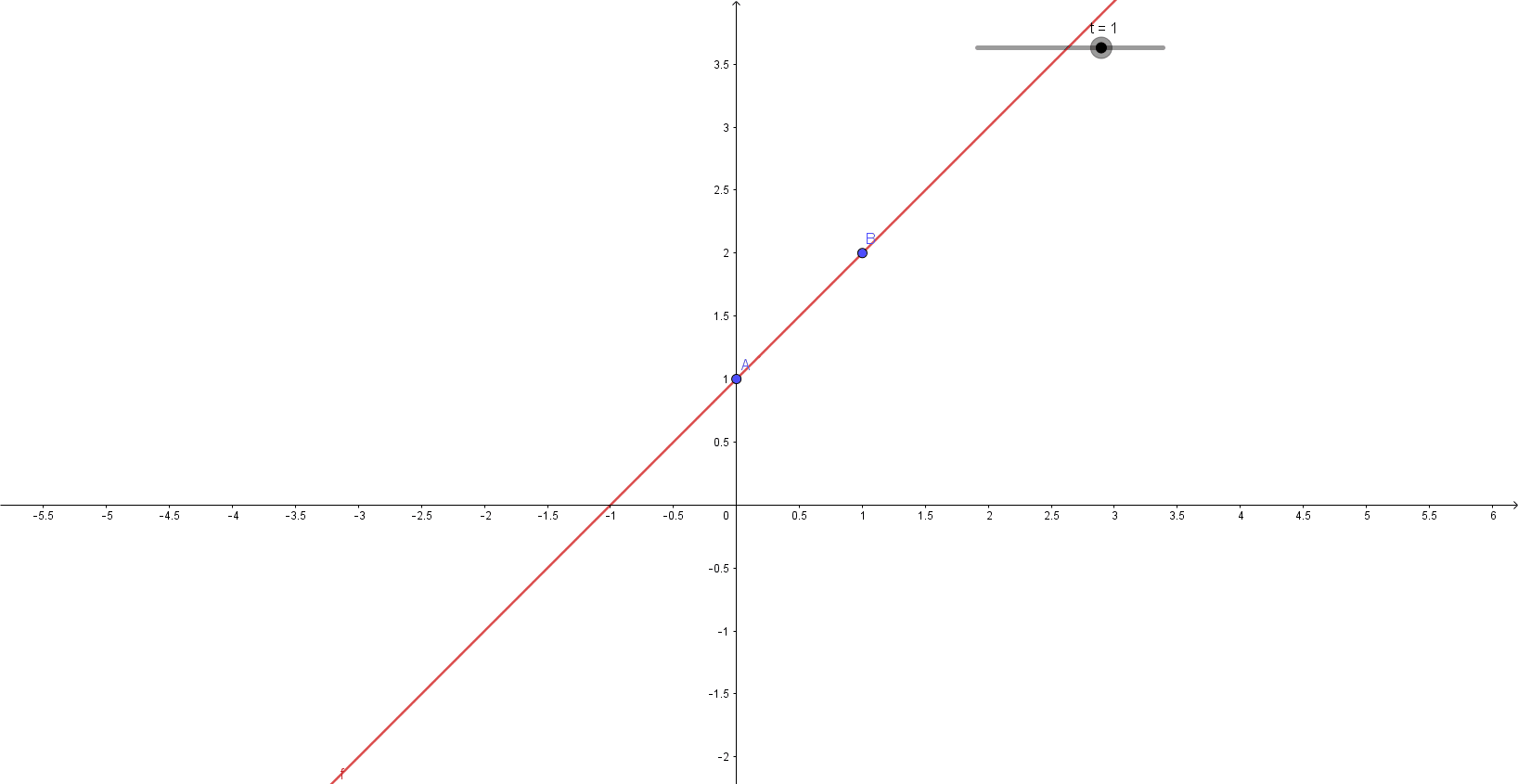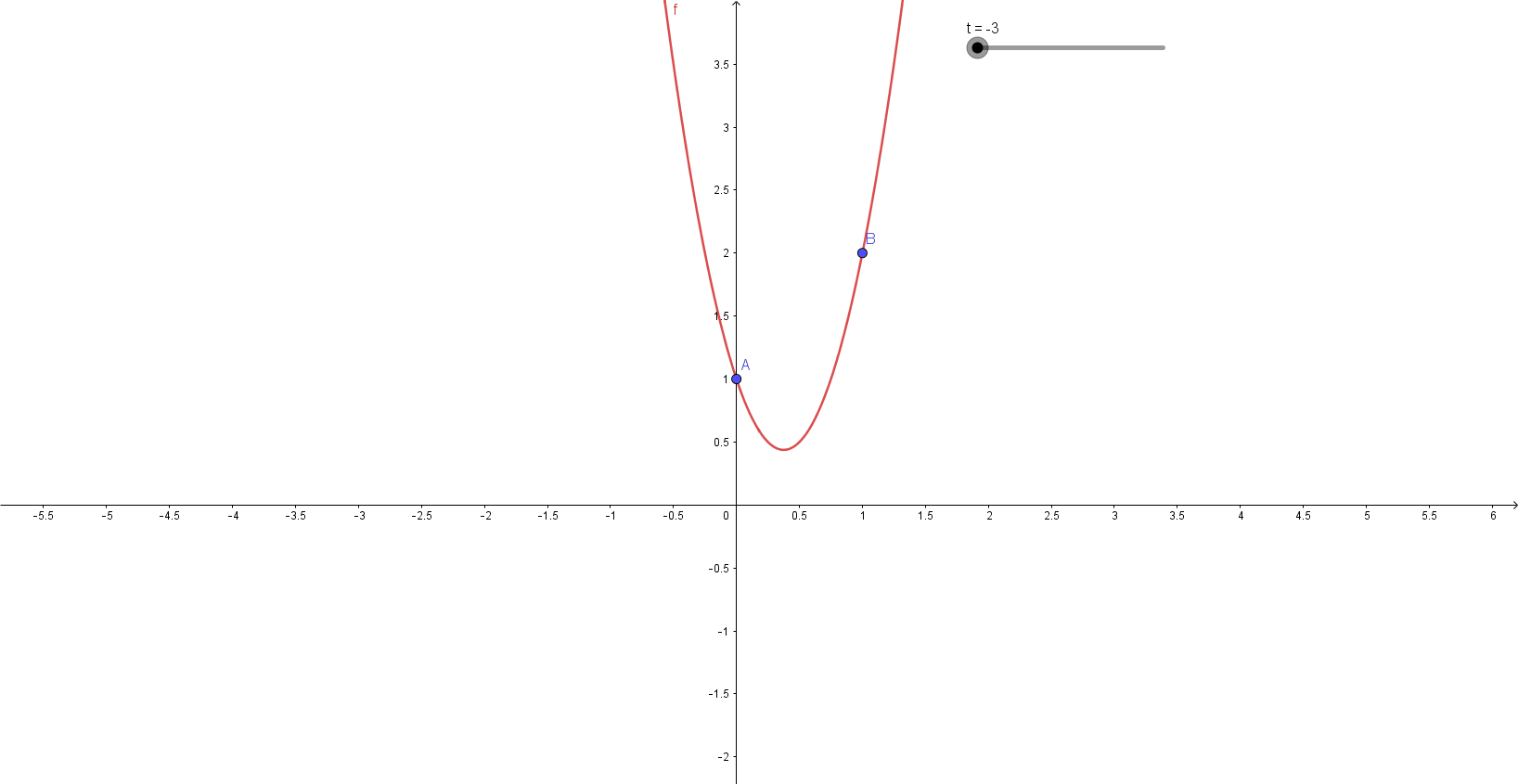
Visual representation of fitting various second-degree polynomials (parabolas) to a pair of (x,y) coordinates created in GeoGebra
As mentioned previously, one of my goals for the initial set of presentations was to convey the importance and value of both real-world and abstract applications of mathematics. The first lecture addressed the former. Throughout various fields of study, fitting curves to sets of data is a necessary component of research and modeling certain phenomena. In particular, I discussed the application of this concept in civil engineering with respect to beam deformation. The second lecture however focused on a less concrete application, where I concluded the presentation with a story from the life of mathematician G.H. Hardy.
Hardy made numerous profound contributions to various STEM fields. In particular, his work with prime numbers represents some of his most notable accomplishments. During that time, Hardy was asked by many about the purpose behind his work. Where could his research be used? What were the goals behind his findings? In response, Hardy published a book called A Mathematician's Apology. Famously, he stated, "I have never done anything "useful". No discovery of mine has made, or is likely to make, directly or indirectly, for good or ill, the least difference to the amenity of the world."
I have never done anything "useful". No discovery of mine has made, or is likely to make, directly or indirectly, for good or ill, the least difference to the amenity of the world.
- G.H. Hardy, A Mathematician's Apology
He argued that the practical application of his work was irrelevant. If an individual has the ability and curiosity to answer the unknown mysteries of science and mathematics, then that should serve as reason enough for further investigation. However, little would he know that only a few decades later, his work would become the foundation for the field of cryptography.
In the end, my hope in telling Hardy's story was to appeal to each student's inherent inquisitive nature, urging them to appreciate the beauty of mathematics, which in turn could lead to incredible discoveries and groundbreaking innovations.